Cryptographic algorithms¶
To ensure the confidentiality of transmitted and processed data, the service uses a set of modern cryptographic algorithms.
The general view of the operation of the cryptographic algorithms of the service is shown in the diagram:
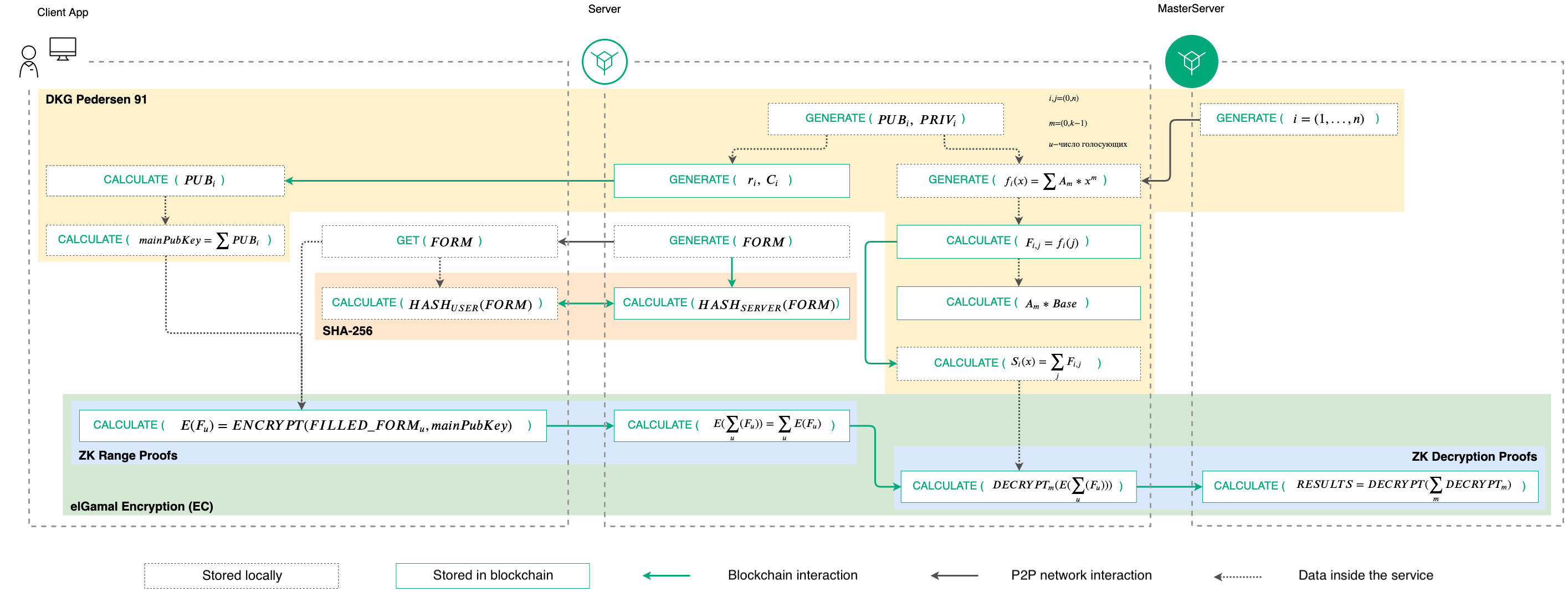
Operation procedures of cryptographic algorithms¶
Generation of keys¶
The interaction of the system components is based on the MPC (Multi-Party Computation) cryptographic protocol, which is used to generate key pairs.
It allows several participants to independently perform cryptographic calculations based on their own secret data, without having information about each other’s secret data. During the computation process, the participants do not exchange secret data, independently generating a set of private keys for the common public public key. This method eliminates a single point of failure: the assembled key pair does not exist on any of the participating servers.
The MPC protocol utilizes the ‘K out of N’ principle corresponding with the Shamir’s Secret Sharing scheme:
decryption does not require all N parties involved in the encryption process: decryption can be done using a smaller threshold number of K parties;
at that,**K - 1** and less parties have no way to decipher the data.
This principle allows the service to work even if several servers in the system fail, while providing a high degree of data protection. Each MPC member server generates its own public and private keys, as well as a general public key (MainPublicKey), exchanging unclassified data about its computations with other members via blockchain transactions.
To generate a public key, the system uses the algorithm of Distributed Key Generation (DKG) made by Torben Pedersen (DKG Pedersen 91), transferred to elliptic curves sexp256k1 and P-256. The generation process involves cryptographic operation services of the system servers, communicating with each other via transactions to their own nodes. For each new vote, the process of generating a new shared public key is started.
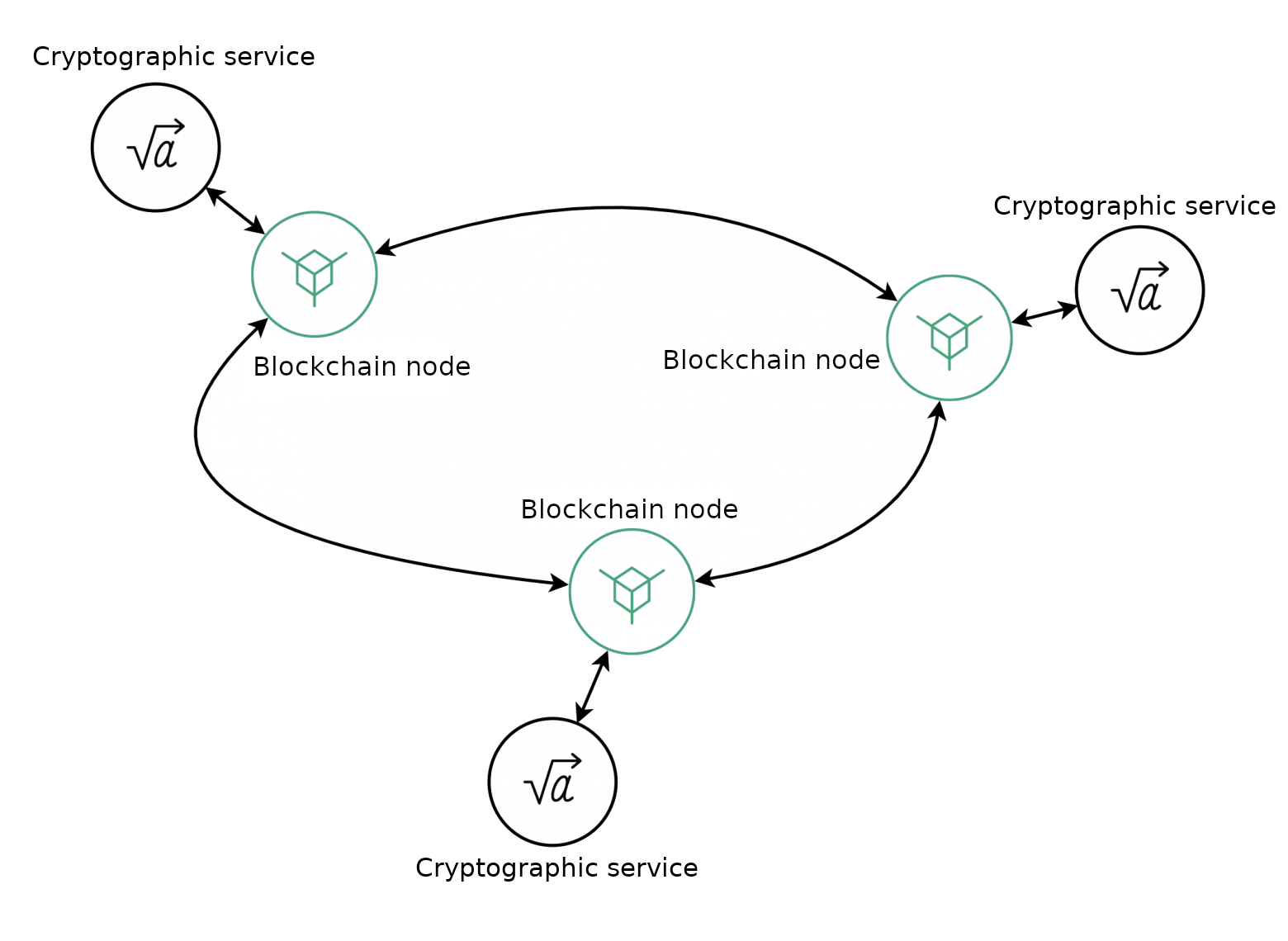
DKG algorithm scheme¶
The process of DKG Pedersen 91 key generation is divided into following steps:
After publishing a new vote, the master server polls available cryptographic services of participating servers. Based on the received data, it forms a list of N services and assigns each of them an ordinal number from 1 to N.
Each cryptographic service generates public and private keys for voting.
Each cryptographic service publishes a Pedersen commit and a corresponding scalar (Ciand ri) to the blockchain. The commitment and the scalar are published for voting participants.
After receiving Ciand ri, each voter (client encryption service) computes the public keys of each cryptographic service.
Based on the public keys, the voting members calculate a common voting key.
To realize the K out of N Shamir’s Secret Sharing scheme, cryptographic services perform following algorithm:
Each cryptographic service randomly generates a fi(x)K - 1polynomial.
Each cryptographic service calculates polynomial values for N other servers according to their ordinal numbers: so called “shadows” F:sub:`i, j.
Cryptographic services publish the calculated “shadows” and polynomial coefficient values for all other servers to the blockchain.
Cryptographic services check the correctness of published “shadows” and calculate the private key needed for decryption.
This process allows to restore the encrypted results of the vote, even if some of the servers are unavailable.
Encryption¶
Ballots are not transferred in an open format within the system. To encrypt them on the client side, the El Gamal cryptosystem based on elliptic curves is used. This cryptosystem implements the homomomorphic encryption method with respect to addition: as a result of the addition operation on the ciphertext, the encryption service generates an encrypted sum of the original values.
To implement this encryption method, each ballot is represented as a matrix, where each row is a separate question, and the row cells are the answer choices to the question. Each of the cells is initially represented as zero, and the answer choices chosen by the participant change the value of the corresponding cell to one. Additionally, each cell of the completed ballot is encrypted and then published to the blockchain.
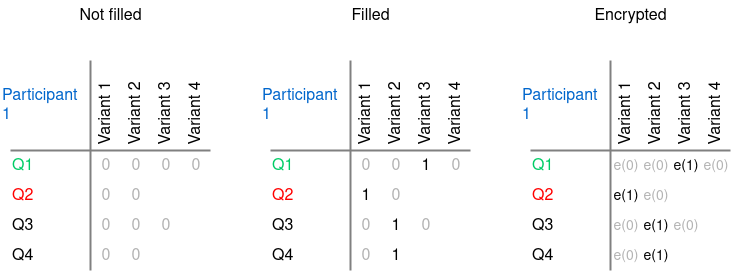
Ballot encryption procedure¶
Then, using homomorphic encryption, the encrypted cells corresponding to each answer choice are summed separately by each server in the system:

Addition of encrypted answers¶
As a result, each of the servers in the system independently receives the voting results without revealing the voting results of participants.
This process solves the following problems faced by online voting:
A participant’s voice cannot be faked: it is not transmitted openly and is not even deciphered.
A participant cannot be forced to vote for one or another option: in addition to complete anonymization of the voting results, the participant has the ability to change their choice during the vote. When counting, the system will only count the last ballot sent on behalf of the participant’s public key.
Zero Knowledge Proofs (ZKP)¶
The El Gamal cryptosystem avoids compromising of voting results by the organizer or an external intruder. However, it does not protect the ballot from being compromised by the voter himself: since an algorithm for adding up the encrypted ballot results is applied, the voter can change the data on the side of his client application. By making changes to the answer choice and sending the “valid” ballot to the system for further encryption and addition, he can achieve the desired number of votes for a planned variant.
Therefore, in addition to encrypted ballots and closed vote counts, the Zero Knowledge Proofs (ZKP) technique is used to prove the integrity of the ballots. This technique allows you to prove possession of information without disclosing it - including the correctness of an encrypted value without disclosing it.
In general, the ZKP principle can be demonstrated by the ‘Ali Baba Cave’ illustration:
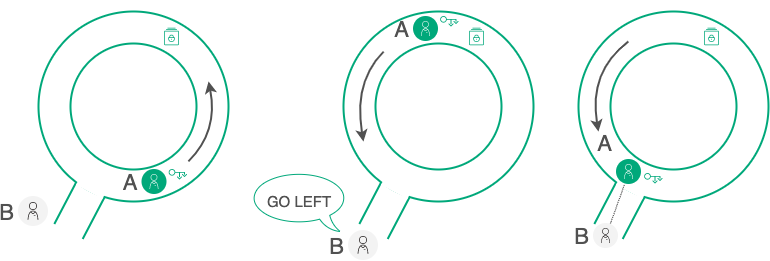
ZKP demonstration¶
An A participant has a key to open a door in the labyrinth and wants to prove this for a B participant without revealing the key itself. For B to be able to verify the correctness of the A statement, they organize a series of tests:
A goes into the labyrinth while B turns his back. B doesn’t know which way A went.
B gives A an instruction to come out on either side, for example on the left.
If A really has a key, it can appear on either side and execute the instructions of B.
The chance that A just got lucky and, not having the key, initially went left is 50/50. So they repeat the test several times until the probability of “luck” is negligible: as a result, B will have sufficient evidence that A does possess the key. In doing so, B will not see the key itself, nor will he get any of the information that A possesses (the direction that A chooses in each trial) - but, through a series of trials, he will get probabilistic proof, with any accuracy necessary.
As applied to the WE.Vote voting process, Non-Interactive Zero-Knowledge Proofs (NIZK)** are used for interaction between participants.
The proof process itself is divided into two algorithms:
1. Zero-Knowledge Range Proofs
This proof is used when the encrypted ballot is published, before the votes are counted.

Zero-Knowledge Range Proof scheme¶
For majority voting, the proof process is following:
A NIZK is added to each cell, proving that the cell contains one of two possible values in an encrypted format: 0 or 1. At that, the value itself is not revealed.
Additionally, each cell contains a proof that the sum of all encrypted cells related to the question is 1.
This will prove, that a participant can set the 1 value in any cell in the row (choose any answer).
For multiple-choice voting, where a participant can choose multiple cells of the row, the process is more complex:
A NIZK for the [0, 1 … N] array is added for each filled and encrypred cell: a participant can choose all N answers, as well as some of them.
Proof of the sum of the cells for a single question can be applied to the range [1…N] (the participant can choose from 1 to N options, but cannot leave the question unanswered), or to the value N (the participant distributes the available votes between the answer choices).
For weighted voting, where each participant casts a number of votes equal to their weight in the system (e.g., proportional to their ownership interest in the company), the proof process is as follows:
Each of the filled and encrypted cells contains a NIZK, proving that the cell contains one of the values in an encrypted form: 0 or N, where N is weight of the participant.
As proof of the sum of the cells, the N value is attached, since in weighted voting the participant can put the N value in one cell in the row, just like in majority voting.
The system only accepts ballots whose ZKPs have passed the authenticity checks in full. That is, an attacker can distort the data in his ballot by taking advantage of the fact that the system does not disclose its contents - however, in this case, the ballot will still fail validation.
2. Zero-Knowledge Decryption Proofs
This proof is used when each service publishes cryptographic operations of the results of the preliminary decryption of the voting results. Since the services operate independently of each other, at this stage there is a danger of data spoofing by one or more individual services. Decryption proofs make it possible to verify that each service decrypted and published exactly the results of performed voting.
To do this, each of the services appends a proof to its decryption result, using the ZKP Chaum-Pedersen algorithm. This algorithm proves the knownness of the number X for two ratios:
A = X * B;
C = X * D.
Here, A, B, C and D are points of one curve.
Due to the attached proof, each qualified spectator can independently perform following operations:
perform homomorphic addition of valid ballots and get the totals of the voting results for comparison;
check the proof of decryption totals from each individual cryptographic service;
conduct a final transcript of the voting results using the public data placed on the blockchain during voting.
Decryption proof eliminates the possibility of data spoofing if one or more of the system’s servers are compromised.