Криптографические алгоритмы

Для обеспечения конфиденциальности передаваемых и обрабатываемых данных, сервис применяет набор современных криптографических алгоритмов.

Общий вид работы криптографических алоритмов сервиса представлен на схеме:

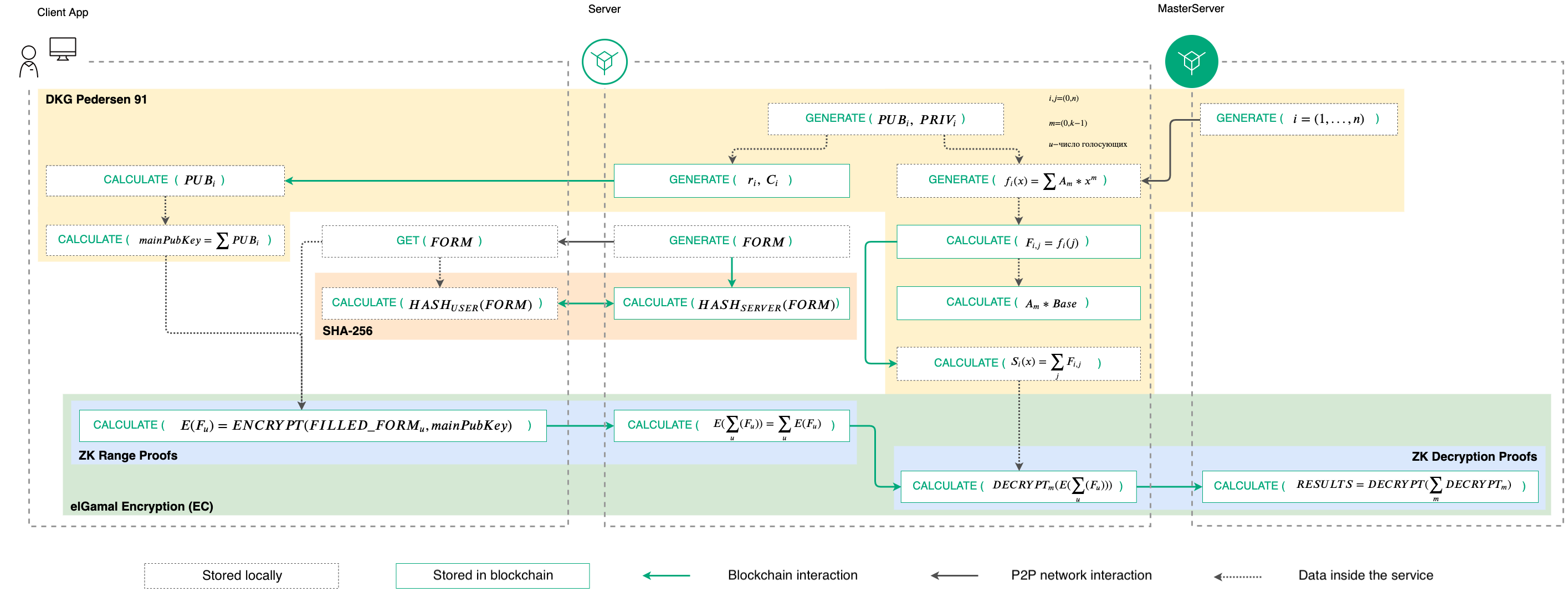
Процедура шифрования данных

Порядок работы криптографических алгоритмов

Генерация ключей

В основе взаимодействия компонентов системы лежит криптографический протокол MPC (Multi-Party Computation), который используется для генерации ключевых пар.

Он позволяет нескольким участникам независимо друг от друга производить криптографические вычисления на основе собственных секретных данных, не имея при этом информации о секретных данных друг друга. В процессе вычисления участники не обмениваются секретными данными, независимо генерируя набор приватных ключей для общего публичного ключа. Такой метод позволяет избавиться от единой точки отказа: в собранном виде ключевая пара не существует ни на одном из серверов-участников.

Применяемый протокол MPC использует принцип «K из N», соответствующий схеме разделения секрета Шамира:

  • для расшифровки данных не требуется участие всех N сторон, участвовавших в процессе шифрования: расшифровка может быть произведена с использованием меньшего порогового количества К сторон;

  • при этом,**K - 1** и менее сторон не имеют возможности расшифровать данные.

Этот принцип позволяет поддерживать работу сервиса даже при нарушении функционирования нескольких серверов системы, при этом обеспечивая высокую степень защиты данных. Каждый из серверов-участников протокола MPC формирует собственные публичный и приватный ключи, а также общий публичный ключ (MainPublicKey), обмениваясь с другими участниками несекретными данными о своих вычислениях при помощи транзакций в блокчейн-сети.

Для формирования общего публичного ключа применяется алгоритм распределенной генерации ключей (Distributed Key Generation, DKG) за авторством Торбена Педерсена (DKG Pedersen 91), перенесенный на эллиптические кривые seсp256k1 и P-256. В процессе генерации участвуют сервисы криптографических операций серверов системы, общаясь друг с другом посредством транзакций на собственные ноды. Для каждого нового голосования запускается процесс генерации нового общего публичного ключа.

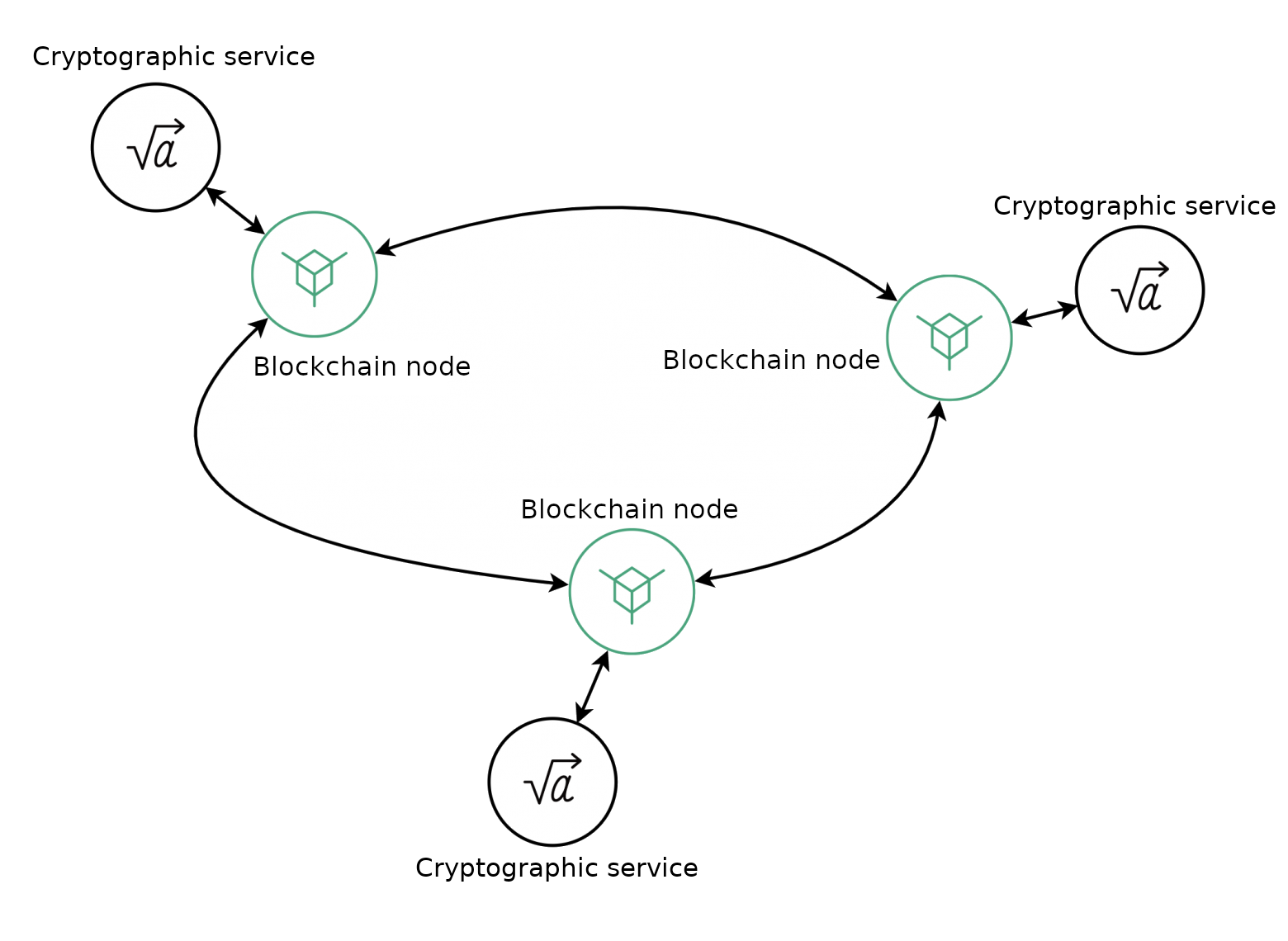
Схема работы алгоритма распределенной генерации ключей

Схема работы алгоритма распределенной генерации ключей

Процесс распределенной генерации общего публичного ключа по DKG Pedersen 91 выглядит следующим образом:

  1. После публикации нового голосования, мастер-сервер опрашивает доступные сервисы криптографических операций серверов-участников. Но основе полученных данных, он формирует список из N сервисов и присваивает каждому из них порядковый номер от 1 до N.

  2. Каждый криптографический сервис генерирует публичный и приватный ключи для участия в голосовании.

  3. Каждый криптографический сервис публикует в блокчейн обязательство (Pedersen commit) и соответствующий скаляр - Ciи ri. Обязательство и скаляр публикуются для участников голосования.

  4. После получения Ciи ri, каждый участник голосования (сервис шифрования клиента) вычисляет публичные ключи каждого криптографического сервиса.

  5. На основе публичных ключей, участники голосования вычисляют общий ключ голосования.

Для реализации схемы разделения секрета Шамира «K из N», сервисы криптографических операций выполняют следующий алгоритм:

  1. Каждый сервис криптографических операций случайным образом генерирует полином fi(x)K - 1.

  2. Каждый сервис криптографических операций вычисляет для N других серверов значения полинома в соответствии с их порядковыми номерами - т.н. «тени» Fi, j.

  3. Сервисы криптографических операций публикуют в блокчейн вычисленные «тени» и значения коэффициентов полиномов для всех остальных серверов.

  4. Сервисы криптографических операций проверяют корректность опубликованных «теней» и вычисляют приватный ключ, необходимый для дешифровки.

Данный процесс позволяет восстановить зашифрованные итоги проведенного голосования, даже если некоторые из серверов будут недоступны.

Шифрование

Бюллетени не передаются в рамках системы в открытом виде. Для их шифрования на стороне клиента применяется криптосистема Эль-Гамаля, также основанная на эллиптических кривых. Эта криптосистема реализует метод гомоморфного шифрования относительно сложения: в результате операции сложения над шифротекстом, сервис шифрования генерирует зашифрованную сумму исходных значений.

\[ENCRYPTED (1) + ENCRYPTED (1) = ENCRYPTED (2)\]

Для реализации этого метода шифрования, каждый бюллетень представляется в виде матрицы, где каждая строка - это отдельный вопрос, а ячейки строки - варианты ответа на вопрос. Каждая из ячеек изначально представлена в виде нуля, а выбранные участником варианты ответов меняют значение соответствующей ячейки на единицу. Дополнительно, каждая ячейка заполненного бюллетеня подвергается шифрованию, после чего публикуется в блокчейн.

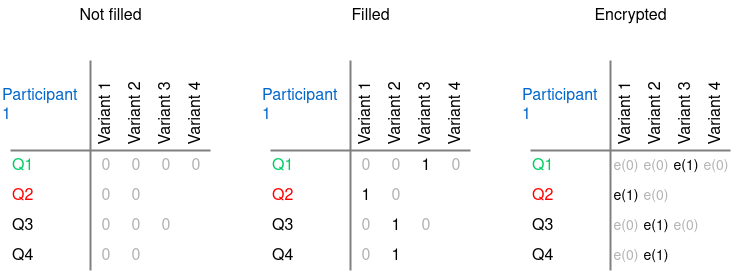
Процедура шифрования бюллетеней

Процедура шифрования бюллетеней

Затем, при помощи гомоморфного шифрования, зашифрованные ячейки, соответствующие каждому из вариантов ответа, суммируются отдельно каждым сервером системы:

Процедура сложения зашифрованных ответов

Процедура сложения зашифрованных ответов

В результате, каждый из серверов системы независимо получает результаты голосования без раскрытия результатов голосования каждого из участников.

Такой процесс позволяет решить следующие проблемы, с которыми сталкиваются онлайн-голосования:

  • Голос участника невозможно подделать: он не передается в открытом виде и даже не расшифровывается.

  • Участника невозможно принудить к голосованию за тот или иной вариант: помимо полной анонимизации результатов голосования, участник имеет возможность изменить свой выбор в ходе голосования. При подсчете система будет учитывать только последний бюллетень, отправленный от имени публичного ключа участника.

Доказательства с нулевым разглашением (ZKP)

Криптосистема Эль-Гамаля позволяет избежать компрометации результатов голосования со стороны организатора или внешнего злоумышленника. Однако, она не защищает бюллетень от компрометации самим участником голосования: поскольку применяется алгоритм сложения зашифрованных результатов голосования, участник может изменить данные на стороне своего клиентского приложения. Внеся изменения в вариант ответа и отправив «валидный» бюллетень в систему для последующего шифрования и сложения, он может добиться нужного числа голосов за тот или иной вариант.

Поэтому, помимо шифрования бюллетеней и закрытого подсчета результатов голосования, для подтверждения целостности бюллетеней применяется техника доказательств с нулевым разглашением (Zero-Knowledge Proofs, ZKP). Эта техника позволяет доказать обладание информацией без ее раскрытия - в том числе, корректность зашифрованного значения без его раскрытия.

В общем виде, принцип работы доказательств с нулевым разглашением иллюстрируется «Пещерой Али-Бабы»:

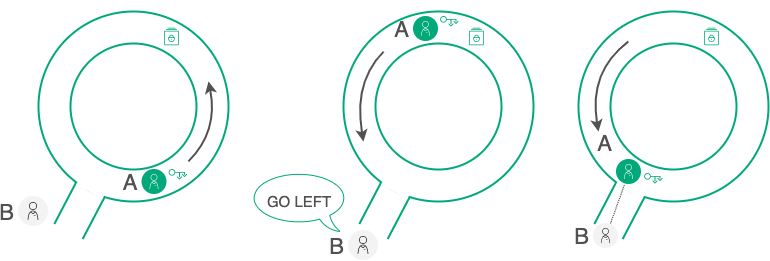
Иллюстрация техники доказательства с нулевым разглашением

Иллюстрация техники доказательства с нулевым разглашением

Участник A обладает ключом, открывающим дверь в лабиринте, и хочет доказать это участнику B, но не хочет показывать ключ. Чтобы В мог убедиться в верности утверждения А, они организуют серию испытаний:

  1. А заходит в лабиринт пока В отвернулся. В не знает в какую сторону пошел А.

  2. В дает А указание выйти с какой-либо стороны, например слева.

  3. Если А действительно обладает ключом, он может появиться с любой стороны и выполняет указание В.

Шанс того, что А просто повезло, и он, не имея ключа, изначально пошел налево составляет 50/50. Поэтому они повторяют испытание несколько раз, пока вероятность «везения» не станет пренебрежимо малой: в результате, В будет располагать достаточными доказательствами, что А действительно обладает ключом. При этом, В не увидит самого ключа, не получит никакой информации, которой обладает А (направление, которое А выбирает в каждом испытании) - но, в результате серии испытаний, он получит вероятностное доказательство, с любой необходимой точностью.

В применении к процессу голосования в системе WE.Vote, для взаимодействия между участниками применяются неинтеркативные доказательства с нулевым разглашением (Non-Interactive Zero-Knowledge Proofs, NIZK).

Сам процесс подтверждения подразделяется на два отдельных алгоритма:

1. Доказательство корректности диапазона в бюллетене (Zero-Knowledge Range Proofs)

Данное доказательство используется при публикации зашифрованного бюллетеня, до начала подсчета голосов.

Иллюстрация доказательства корректности диапазона в бюллетене

Иллюстрация доказательства корректности диапазона в бюллетене

Для мажоритарного голосования, процесс доказательства выглядит следующим образом:

  1. К каждой из заполненных и зашифрованных ячеек прикладывается NIZK, доказывающее, что в ячейке зашифровано одно из значений - 0 или 1. При этом, само значение не раскрывается.

  2. Дополнительно, к каждой из ячеек прикладывается доказательство, что зашифрованная сумма всех ячеек строки-вопроса равна 1.

Таким образом, подтверждается, что участник голосования может поставить значение 1 в одну ячейку в ряду (выбрать один из предложенных вариантов ответа).

Для голосования с множественным выбором, где участник может выбрать несколько ячеек строки, процесс усложняется:

  1. К каждой заполненной и зашифрованной ячейке прикладывается NIZK для диапазона [0, 1 … N] - участник может выбрать как все N вариантов ответа, так и некоторые из них.

  2. Доказательство суммы ячеек по отдельному вопросу может приклдываться для диапазона [1…N] (участник может выбрать от 1 до N вариантов, но не может оставить вопрос без ответа), либо для значения N (участник распределяет доступное количество голосов между вариантами ответа).

Для взвешенного голосования, когда каждый участник отдает количество голосов, равное его весу в системе (например, пропорциональное доле владения в компании), процесс доказательства выглядит следующим образом:

  1. К каждой из заполненных и зашифрованных ячеек прикладывается NIZK, доказывающее, что в ячейке зашифровано одно из значений - 0 или N, где N - вес участника.

  2. В качестве доказательства суммы ячеек, прикладывается значение N, поскольки при взвешенном голосовании участник может поставить значение N в одну ячейку в ряду, как и при мажоритарном голосовании.

Система принимает к подсчету только те бюллетени, все ZKP которых прошли проверку подлинности. То есть, злоумышленник может исказить данные в своем бюллетене, воспользовавшись тем, что система не раскрывает его содержимого - однако, в таком случае бюллетень все равно не пройдет валидацию.

2. Доказательство расшифровки (Zero-Knowledge Decryption Proofs)

Данное доказательство применяется при публикации каждым сервисом криптографических операций результатов предварительной расшифровки итогов голосования. Поскольку сервисы действуют независимо друг от друга, на этом этапе существует опасность подмены данных одного или нескольких отдельных сервисов. Доказательство расшифровки позволяет убедиться, что каждый сервис расшифровал и опубликовал именно результаты голосования, а не иную информацию.

Для этого каждый из сервисов прикладывает к своему результату расшифровки доказательство, используя алгоритм ZKP Chaum-Pedersen. Этот алгоритм доказывает известность числа X для двух соотношений:

  • A = X * B;

  • C = X * D.

При этом, A, B, C и D являются точками, лежащими на одной кривой.

Благодаря приложенному доказательству, любой квалифицированный наблюдатель может самостоятельно произвести следующие операции:

  • выполнить гомоморфное сложение валидных бюллетеней и получить итоговые суммы результатов голосования для сравнения;

  • проверить доказательства расшифровки итоговых сумм от каждого отдельного сервиса криптографических операций;

  • провести итоговую расшифровку результатов голосования с использованием публичных данных, размещенных в блокчейне в ходе голосования.

Доказательство расшифровки исключает вероятность подмены данных при компрометации одного или нескольких серверов системы.